Uma Dança Cósmica Revelada: ALMA Desvenda o Segredo da Excentricidade do Disco de Detritos de Fomalhaut e Reimagina a Formação Planetária

Introdução: O Convite para o Espanto Cósmico 

Queridos amantes do cosmos e exploradores das maravilhas do universo, preparem-se para uma jornada fascinante que nos levará às profundezas da formação planetária, desvendando segredos de um dos sistemas estelares mais icônicos e estudados em nossa vizinhança cósmica: Fomalhaut. Imagine um balé celestial, onde planetas e detritos dançam ao redor de uma estrela brilhante, moldando uns aos outros em uma coreografia intrincada que se desenrola por milhões e até bilhões de anos. Por muito tempo, os astrônomos têm se maravilhado com a complexidade desses sistemas, tentando decifrar as regras ocultas que governam a sua evolução. Como se formam os planetas? Como os anéis de poeira e rocha que os cercam, conhecidos como discos de detritos, são esculpidos ao longo do tempo? Essas são perguntas fundamentais que impulsionam a busca incansável por conhecimento no campo da astrofísica.

E hoje, temos uma notícia que não apenas responde a algumas dessas perguntas para o sistema Fomalhaut, mas também nos força a reconsiderar modelos antigos e abraçar uma nova e mais profunda compreensão da dinâmica dos discos planetários. Graças ao poder incomparável do Atacama Large Millimeter/submillimeter Array (ALMA), uma equipe de pesquisadores liderada por Joshua B. Lovell fez uma descoberta que está redefinindo o que sabemos sobre o disco de detritos de Fomalhaut: a primeira evidência clara de um gradiente negativo de excentricidade. Este não é apenas um termo técnico complicado; é a chave para desvendar a história de vida deste disco e, possivelmente, de muitos outros em nossa galáxia.

Por que isso é tão emocionante? Porque Fomalhaut não é uma estrela qualquer. Situada a apenas 7,66 parsecs (aproximadamente 25 anos-luz) de nós, é uma das estrelas de tipo A mais próximas e bem estudadas, um verdadeiro laboratório natural para a formação de planetas. Seu disco de detritos tem sido observado com uma miríade de telescópios, desde o Hubble até o James Webb, revelando estruturas complexas e assimetrias que desafiam uma explicação simples. Agora, com este novo estudo, estamos um passo mais perto de montar o quebra-cabeça cósmico, entendendo como as interações gravitacionais de planetas e as propriedades intrínsecas do disco atuam para criar as belas e enigmáticas formas que observamos. Esta é uma história de persistência científica, de tecnologia de ponta e, acima de tudo, da incessante busca humana por compreender nosso lugar no vasto e maravilhoso universo. Preparem-se para se apaixonar ainda mais pela astronomia!

1. O Enigma de Fomalhaut: Um Clássico da Astronomia com Novas Revelações

Fomalhaut, cujo nome deriva do árabe “fam al-hūt (al-janūbī)”, que significa “a boca da (baleia) do sul”, é uma estrela que há muito tempo captura a imaginação de astrônomos e entusiastas. É a estrela mais brilhante da constelação austral de Peixe Austral e um farol no estudo de discos de detritos. Desde que seu disco de detritos foi descoberto em 1985, através de análises das observações do Infrared Astronomical Satellite (IRAS), Fomalhaut tem sido um objeto de estudo intensivo e de grande interesse.

Ao longo das décadas, a tecnologia de observação avançou exponencialmente, permitindo aos cientistas resolver o disco de Fomalhaut com uma resolução cada vez maior. O Telescópio Espacial Hubble (HST) revelou detalhes no óptico em luz espalhada. O Telescópio Espacial Spitzer e, mais recentemente, o revolucionário Telescópio Espacial James Webb (JWST), nos trouxeram visões em emissão térmica no infravermelho próximo e médio. O Telescópio Espacial Herschel contribuiu com observações no infravermelho distante. E, crucialmente para este estudo, o James Clerk Maxwell Telescope e o ALMA nos proporcionaram imagens espetaculares em emissão térmica (sub)milimétrica.

Essas observações coletivas revelaram que o disco de detritos de Fomalhaut não é um anel perfeitamente circular e simétrico. Longe disso! Ele apresenta uma série de assimetrias que indicam uma natureza excêntrica. Por exemplo, a estrela não está no centro geométrico do disco, um indicador clássico de excentricidade. Além disso, o disco exibe assimetrias de brilho dependentes do comprimento de onda. No infravermelho, observamos o que é conhecido como “brilho do pericentro”, onde a parte mais próxima da estrela é mais brilhante. Por outro lado, na emissão milimétrica, observamos o “brilho do apocentro”, onde a parte mais distante é mais proeminente. Essas características são esperadas dadas as condições térmicas e estruturais do disco de Fomalhaut nas resoluções observadas.

Mais recentemente, estudos de G. M. Kennedy (2020) e J. Chittidi et al. (2025) trouxeram evidências de uma assimetria na largura do disco, com uma largura maior no pericentro (ponto mais próximo da estrela) em comparação com o apocentro (ponto mais distante). Todas essas observações, juntas, comprovam a natureza excêntrica do disco de detritos de Fomalhaut. No entanto, o que este novo trabalho de Lovell et al. (2025) adiciona é uma camada de complexidade e entendimento sem precedentes: a revelação de um gradiente de excentricidade forçada que varia com o semieixo maior. Em termos mais simples, a excentricidade do disco não é constante; ela muda dependendo de quão longe você está da estrela, e essa mudança não é arbitrária, mas segue um padrão específico. Esta descoberta não é apenas um detalhe técnico; é uma nova lente através da qual podemos ver a história e a dinâmica do sistema Fomalhaut.

2. Decifrando a Arquitetura do Disco de Detritos: O Conceito de Gradiente de Excentricidade

Para realmente apreciar a magnitude da descoberta de Lovell e sua equipe, precisamos entender alguns conceitos fundamentais. Primeiro, o que são exatamente os discos de detritos? Imagine os cinturões de asteroides e o Cinturão de Kuiper em nosso próprio Sistema Solar. Discos de detritos são, em essência, cinturões de poeira fria (com temperaturas de dezenas de Kelvin) formados por colisões mútuas de planetesimais – os “blocos de construção” de planetas. Embora essas colisões moam os discos ao longo do tempo, transformando objetos maiores em poeira fina, eles podem sobreviver por centenas e milhares de milhões de anos, produzindo assinaturas de poeira observáveis que os astrônomos podem detectar. São, portanto, relíquias da formação planetária, oferecendo pistas cruciais sobre o ambiente onde os planetas nasceram e evoluíram.

Agora, vamos falar sobre excentricidade. Na astronomia, a excentricidade descreve o quão “esticada” ou elíptica é uma órbita em comparação com um círculo perfeito. Uma órbita circular tem excentricidade zero, enquanto órbitas mais alongadas têm valores maiores. Em muitos sistemas planetários, e especialmente em discos de detritos, as interações entre planetas e os pequenos corpos do disco podem alterar significativamente as estruturas desses discos. Isso pode acontecer de várias maneiras, como o esgotamento, o superpovoamento ou o empenamento das distribuições de planetesimais.

Em escalas de tempo seculares (ou seja, longos períodos de tempo), planetas excêntricos podem “forçar” suas próprias excentricidades nas órbitas dos planetesimais através de interações gravitacionais de três corpos (estrela-planeta-planetesimal). Existem dois tipos principais de excentricidade que são importantes para entender:

• Excentricidade Forçada (ef): É a excentricidade que um planeta, ou um conjunto de planetas, impõe gravitacionalmente sobre as órbitas dos planetesimais. É um valor que é “herdado” da perturbação gravitacional.
• Excentricidade Livre (ep): Também conhecida como excentricidade própria, é a parte da excentricidade de uma órbita que não é forçada por perturbações externas. Ela representa a excentricidade “original” ou “natural” da órbita de um planetesimal, que pode precessar (mudar de orientação) ao longo do tempo.

Em observações resolvidas de discos, características como o deslocamento estelar do centro do disco, assimetrias de brilho e assimetrias de largura foram todas interpretadas como métricas para derivar as excentricidades do disco e suas distribuições. Para Fomalhaut, a excentricidade de seu disco já era conhecida, mas a grande inovação deste estudo é a descoberta de um gradiente de excentricidade.

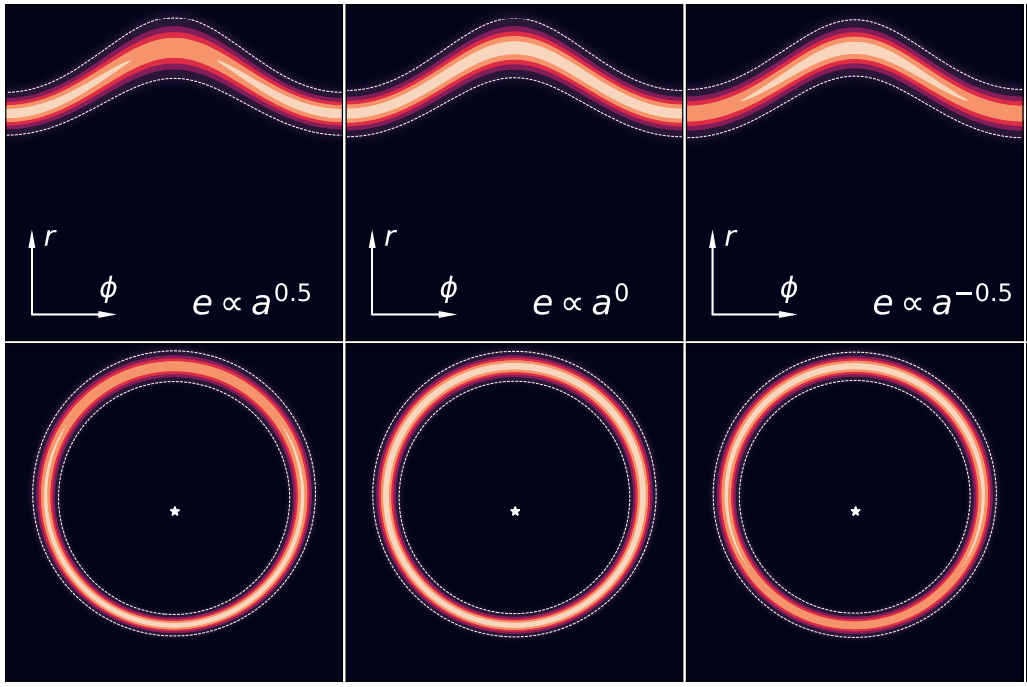
O que significa um gradiente de excentricidade? Significa que a excentricidade forçada (ef) não é um valor único para todo o disco, mas sim uma função da distância à estrela (o semieixo maior, ‘a’). Ela pode ser descrita por uma lei de potência: ef(a) ∝ a^npow. O expoente ‘npow’ é crucial aqui:

• npow = 0 (Gradiente Plano): A excentricidade é constante em todo o disco, ou seja, ∂ef/∂a = 0.
• npow > 0 (Gradiente Positivo): A excentricidade aumenta com a distância da estrela (∂ef/∂a > 0).
• npow < 0 (Gradiente Negativo): A excentricidade diminui com a distância da estrela (∂ef/∂a < 0).

A equipe de Lovell et al. descobriu que o disco de Fomalhaut apresenta um gradiente negativo de excentricidade forçada, com um valor de npow = -1.75 ± 0.16. Isso é uma virada de jogo, pois modelos anteriores muitas vezes presumiam excentricidades constantes ou não exploravam a complexidade de um gradiente. A implicação de um gradiente negativo é que a excentricidade é maior nas partes mais internas do disco e diminui à medida que nos afastamos da estrela. Este perfil de excentricidade tem um impacto profundo na forma como vemos o disco, afetando sua densidade de superfície e suas larguras em diferentes pontos de sua órbita. Esta é a primeira vez que um gradiente de excentricidade é reportado em um disco de detritos, tornando a descoberta um marco significativo.

3. Divergência de Velocidade Excêntrica (EVD): A Chave para Compreender Fomalhaut

A descoberta de um gradiente negativo de excentricidade não é apenas uma curiosidade matemática; ela tem implicações físicas profundas que explicam as características observadas no disco de Fomalhaut. Os autores do estudo introduziram o termo “Divergência de Velocidade Excêntrica” (EVD) para descrever coletivamente o impacto combinado do gradiente de excentricidade na densidade de superfície e na largura do disco. Em sua essência, o EVD surge da continuidade de massa em discos excêntricos.

Para entender o EVD, precisamos visualizar como a excentricidade afeta a distribuição de material em um disco. Modelos anteriores, como os de E. M. Lynch & J. B. Lovell (2021), já haviam demonstrado que perfis de excentricidade forçada em lei de potência (e ∝ a^npow) alteram as densidades de superfície e as morfologias de emissão resultantes. O que foi observado é que:

• Discos com gradientes positivos de excentricidade (npow > 0) tendem a ter suas densidades de superfície aumentadas no pericentro (o ponto mais próximo da estrela).
• Discos com gradientes negativos de excentricidade (npow < 0), como o de Fomalhaut, têm suas densidades de superfície elevadas no apocentro (o ponto mais distante da estrela).

Além disso, esses modelos mostram que as larguras do disco diminuem onde ele é mais denso e se alargam onde ele é menos denso. Portanto, um gradiente negativo de excentricidade faz com que o disco se alargue preferencialmente no pericentro e se estreite preferencialmente no apocentro. Essas são exatamente as características observadas no disco de Fomalhaut: uma largura maior no pericentro em comparação com o apocentro, e densidades de superfície maiores no apocentro em relação ao pericentro. A descoberta do gradiente negativo de npow = -1.75 ± 0.16 para Fomalhaut é, portanto, diretamente consistente com o efeito EVD e explica elegantemente as assimetrias complexas que os astrônomos têm observado por anos.

A análise matemática do efeito na largura do disco mostra que as larguras do apocentro (Δrapo) e do pericentro (Δrperi) dependem dos gradientes de excentricidade. Para o caso geral onde e = e(a), a relação Δrapo > Δrperi só é verdadeira se ∂e/∂a ≳ -e/a. No caso de uma lei de potência e ∝ a^npow, isso significa que Δrapo > Δrperi é verdadeiro apenas se npow ≳ -1. A excentricidade do disco de Fomalhaut, com npow = -1.75, está em um regime onde as larguras no pericentro podem ser maiores que no apocentro, como observado.

Mas de onde vêm esses perfis de excentricidade em lei de potência? Eles são fisicamente motivados! Em situações idealizadas de sistemas de três corpos (estrela, planeta e planetesimal), as interações gravitacionais podem prever relações analíticas entre os semieixos maiores e as excentricidades do planeta perturbador e dos planetesimais. Por exemplo, para um perturbador planetário interno (um planeta mais perto da estrela que o disco), espera-se uma relação ef(a) ∝ a^-1. Para um perturbador externo (um planeta mais longe da estrela), a relação esperada é ef(a) ∝ a. Esses gradientes podem se tornar mais acentuados quando o semieixo maior de um planeta perturbador se aproxima dos planetesimais ou se os planetesimais são modelados com massa (ou seja, se a auto-gravidade do disco é considerada). Gradientes de excentricidade semelhantes são observados no Cinturão de Kuiper, onde a distribuição de Objetos Trans-Netunianos exibe perfis íngremes de ef(a). A plausibilidade de tais distribuições de excentricidade ser descrita pelo efeito EVD é reforçada por trabalhos teóricos em discos protoplanetários (de gás), que mostram que gradientes de excentricidade são necessários para evitar a precessão diferencial violenta em discos com excentricidade constante. Se os discos de detritos se formam a partir de material primordial com essas distribuições de excentricidade, ou são moldados por interações planeta-disco excêntricas, é plausível que suas estruturas sejam bem descritas pelo efeito EVD.

4. A Tecnologia por Trás da Descoberta: ALMA e Modelagem Avançada

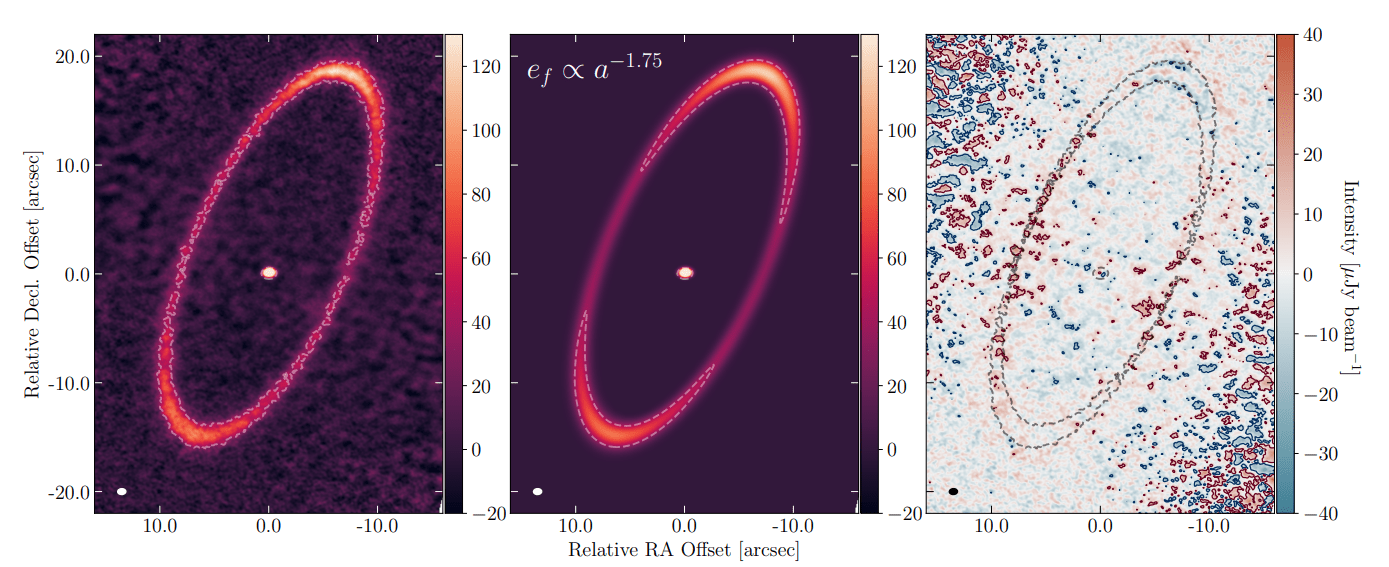
A revelação do gradiente de excentricidade em Fomalhaut não seria possível sem a combinação de observações de alta resolução e técnicas de modelagem computacional sofisticadas. No centro desta pesquisa estão os dados de 1.32 mm do ALMA, apresentados por J. Chittidi et al. (2025). O ALMA, com sua impressionante resolução angular de 0,76 x 0,55 (equivalente a 4-6 unidades astronômicas na distância de Fomalhaut), permitiu à equipe de Lovell et al. examinar os detalhes do disco como nunca antes.

As observações do ALMA foram combinadas a partir de três conjuntos de dados (P.I.s: Aaron Boley, Paul Kalas, e Meredith MacGregor), calibrados e alinhados usando procedimentos padrão do CASA ALMA. As imagens resultantes, com uma resolução física de 6 x 4 au na distância de Fomalhaut, fornecem a base para o estudo. É importante notar que a imagem final do ALMA apresenta propriedades de ruído não-gaussianas devido à combinação de diferentes configurações e sensibilidades, sendo mais ruidosa perto do eixo menor do disco. Para lidar com isso, a equipe utilizou uma máscara de ajuste, focando nas regiões de alto sinal-ruído (SNR) do disco e evitando artefatos de imagem e fontes de fundo.

Para interpretar esses dados complexos, a equipe produziu modelos paramétricos de discos opticamente finos, utilizando o framework RADMC-3D (C. P. Dullemond et al. 2012). O modelo de disco assumiu parâmetros estelares para Fomalhaut (temperatura efetiva, raio estelar, massa estelar), uma distribuição de tamanho de poeira e uma distribuição gaussiana de semieixo maior. O ponto crucial foi a inclusão de um parâmetro de gradiente de excentricidade forçada (npow), permitindo que a excentricidade variasse com a distância da estrela na forma e_f(a) ∝ a^npow.

A equipe usou o método de Monte Carlo de Cadeia de Markov por Ensemble (MCMC) “emcee” (J. Goodman & J. Weare 2010; D. Foreman-Mackey et al. 2013) para ajustar seus modelos aos dados do ALMA. Esse método é extremamente poderoso para explorar o espaço de parâmetros e encontrar a melhor combinação que descreve as observações. O processo de ajuste foi meticuloso, com várias etapas e verificações para garantir a convergência dos modelos.

Um dos resultados mais importantes desse processo de modelagem foi a determinação significativa do índice de lei de potência do gradiente de excentricidade forçada: npow = -1.75 ± 0.16. Esse valor, que descreve como a excentricidade diminui acentuadamente com a distância da estrela, é o pilar da nova interpretação do disco de Fomalhaut. Os outros parâmetros do disco (massa, semieixo maior, largura, excentricidade média, argumento do pericentro, inclinação e razão de aspecto vertical) também foram determinados com precisão e são consistentes com trabalhos anteriores.

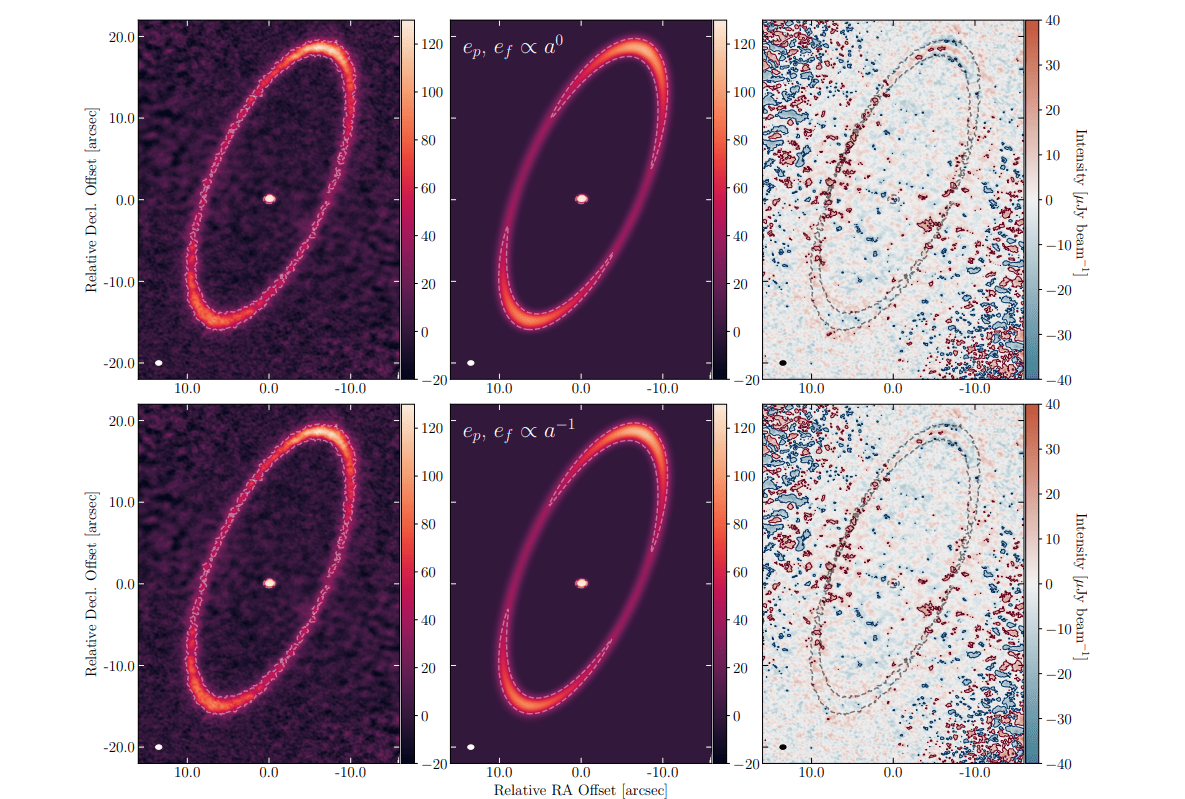
Para validar sua descoberta, os pesquisadores compararam o “Modelo Geral” (com o gradiente de excentricidade) com outros modelos que incluíam a excentricidade livre (ep) e perfis de excentricidade forçada constante (npow = 0) ou fixados em npow = -1. Esses foram chamados de “Proper 1” (npow = 0) e “Proper 2” (npow = -1). O Modelo Geral foi estatisticamente preferido de forma significativa. Em termos de intervalos de confiança, o Modelo Geral foi favorecido sobre o Proper 1 por 6.7σ e sobre o Proper 2 por 2.6σ. Isso significa que a probabilidade de o Modelo Geral ser uma descrição melhor dos dados é extremamente alta. A preferência pelo Modelo Geral é tão forte que, mesmo em uma análise mais rigorosa no domínio das visibilidades (que exige um tempo computacional dez vezes maior), o Modelo Geral ainda se mostrou superior.

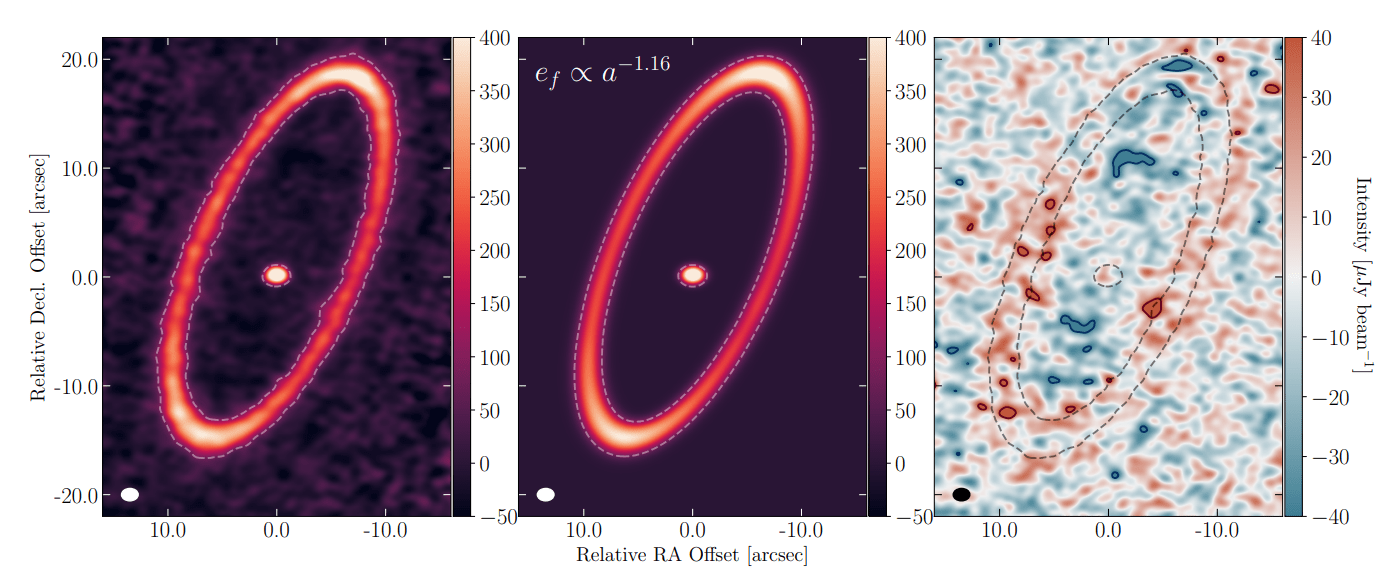
Além disso, a metodologia de ajuste foi verificada ajustando um modelo a dados ALMA de menor resolução de M. A. MacGregor et al. (2017) e G. M. Kennedy (2020). Impressionantemente, mesmo com esses dados de menor resolução, um gradiente negativo de excentricidade (npow = -1.16 ± 0.16) ainda era necessário para ajustar as assimetrias de largura e brilho do disco. Isso sugere que as evidências de um gradiente de excentricidade em Fomalhaut já existiam antes das observações de alta resolução, mas só agora foram formalmente identificadas e quantificadas.

A capacidade do Modelo Geral de explicar as assimetrias observadas – pericentro mais largo e tênue, e pico de brilho no apocentro – dentro do ruído das observações é uma prova de sua eficácia. Pequenos resíduos remanescentes, como um leve excesso de “sub-subtração” na borda externa do apocentro, podem sugerir a necessidade de um gradiente de excentricidade ainda mais acentuado, mas os dados atuais não o preferem estatisticamente. No entanto, a ausência de resíduos positivos significativos nas ansas do disco, ao contrário de modelos anteriores, reforça a robustez da nova interpretação baseada no EVD.

5. O Planeta Escondido? Implicações para o Sistema Planetário de Fomalhaut

A inferência de um gradiente de excentricidade no disco de Fomalhaut tem implicações profundas para a presença e as propriedades orbitais de um planeta interno que interage com o disco. A grande questão é: que tipo de planeta poderia ter esculpido um disco com um gradiente de excentricidade tão específico?

A equipe de Lovell et al. explorou dois cenários plausíveis de um único planeta coplanar que poderiam ser responsáveis por esculpir a estrutura observada do disco (sua localização da borda interna, excentricidade e gradiente de excentricidade). Essas investigações são consistentes com as restrições impostas por observações recentes. As observações do instrumento NIRCam do JWST em Fomalhaut, por exemplo, limitam as massas planetárias (Mpl) a menos de aproximadamente 200 massas terrestres (M⊕) além de 5 segundos de arco (cerca de 38.3 au) do centro estelar. A análise dos cenários de planeta único do estudo está bem abaixo desse limite do NIRCam, o que significa que o planeta proposto não teria sido detectado pelas observações do JWST NIRCam.

Talvez mais importantes para restringir as propriedades planetárias sejam as observações do JWST MIRI (A. Gáspár et al. 2023). Estas observações revelaram a primeira evidência de um “cinturão intermediário” em Fomalhaut, com bordas internas e externas de 83 au e 104 au, respectivamente, e excentricidades correspondentes de 0.31 e 0.265. Assumindo que um planeta não poderia residir dentro da região ocupada por este cinturão intermediário, mas sim entre o “cinturão principal” observado pelo ALMA e o cinturão intermediário, ou internamente ao cinturão intermediário, os pesquisadores puderam derivar propriedades planetárias.

5.1. Cenário 1: Um Planeta Esculpindo a Lacuna (Tipo “Gap-carving”)

Neste cenário, um único planeta teria esculpido diretamente a lacuna até a borda interna do disco principal. Usando uma equação que relaciona o semieixo maior e a excentricidade do planeta com os da borda interna do disco (Equação 10 de A. J. Mustill & M. C. Wyatt (2012)), a equipe calculou que um planeta com massa variando de aproximadamente 1 a 16 massas terrestres (M⊕) — justificada por sua capacidade de forçar secularmente a excentricidade no disco e sua capacidade de limpar material — exigiria semieixos maiores na faixa de 109 a 115 au e excentricidades na faixa de 0.18 a 0.20. O semieixo maior mais interno nessa faixa corresponderia aos valores mais altos de excentricidade e massa planetária. Esses valores foram baseados em uma borda interna do disco principal de aproximadamente 125 au e uma excentricidade de disco estimada em cerca de 0.16 nessa localização, extrapolada a partir dos valores ajustados do gradiente de excentricidade.

É fascinante notar que os parâmetros orbitais deste “Planeta da Lacuna” concordam com aqueles apresentados para Fomalhaut b (P. Kalas et al. 2008), o controverso planeta previamente detectado e posteriormente questionado. Embora observações mais recentes sugiram que Fomalhaut b pode não estar mais presente (A. Gaspar & G. Rieke 2020; M. Ygouf et al. 2024), esta análise sugere que um planeta com propriedades consistentes com o que se pensava ser Fomalhaut b ainda poderia estar presente no sistema e ser o responsável pela escultura do disco. Se o cinturão intermediário não for um cinturão de planetesimais de longa duração, as restrições de massa do JWST NIRCam permitiriam que o planeta tivesse um semieixo maior e excentricidades ligeiramente mais amplos (100-120 au e 0.18-0.23, respectivamente).

5.2. Cenário 2: Um Planeta em Ressonância (Tipo “Resonant-clearing”)

O cinturão intermediário de Fomalhaut apresenta outro cenário plausível: a lacuna entre o cinturão principal e o cinturão intermediário pode ter sido limpa por interações de ressonância de um planeta interno. Para isso, o planeta precisaria estar localizado internamente a 83 au (a borda interna do cinturão intermediário com excentricidade de 0.31) e ter uma ressonância forte (como a ressonância de movimento médio 2:1) situada entre a borda interna do cinturão principal e a borda externa do cinturão intermediário.

Para que a ressonância 2:1 do planeta estivesse a 2 au do ponto médio entre essas localizações dos cinturões, o planeta teria que ter um semieixo maior entre 70 e 75 au. Essa faixa de semieixo maior, por sua vez, exige uma faixa mais estreita de massas planetárias, de aproximadamente 7 × 10^-6 a 2.5 × 10^-5 massas estelares (M*), para que esses planetas sejam responsáveis pela excentricidade na borda interna do cinturão intermediário (utilizando a mesma equação com einner = 0.31). Se esses corpos também seguissem o gradiente de excentricidade em lei de potência, suas excentricidades estariam na faixa de 0.38 a 0.41.

Este “Planeta Ressonante” poderia plausivelmente impulsionar excentricidades maiores no cinturão intermediário, dadas suas proximidades de semieixo maior. Extrapolando a lei de potência de excentricidade ajustada para os semieixos maiores do cinturão intermediário (83-104 au), os pesquisadores calcularam excentricidades na faixa de 0.22-0.32, o que se sobrepõe razoavelmente bem aos valores ajustados às bordas interna e externa do cinturão intermediário observadas pelo JWST (0.31 e 0.265, respectivamente). Assim, a análise do JWST corrobora que Fomalhaut hospeda uma distribuição de excentricidade que diminui com o semieixo maior, o que é um achado notável. Em ambos os cenários, as massas e semieixos maiores implicados para os planetas estão abaixo dos limites de sensibilidade das metodologias de detecção planetária existentes.

6. A Origem da Excentricidade: N-corpos e o Passado de Fomalhaut

Com a evidência de um gradiente de excentricidade e os possíveis cenários planetários, a próxima pergunta crucial é: como essa excentricidade se originou e como o disco de Fomalhaut manteve sua estrutura ao longo de seus 440 milhões de anos de idade? Para investigar isso, os pesquisadores realizaram simulações N-corpos detalhadas do disco de detritos de Fomalhaut usando o código REBOUND (H. Rein & S. F. Liu 2012).

As simulações N-corpos modelam as interações gravitacionais de múltiplos corpos ao longo do tempo. Neste estudo, a equipe simulou um sistema estrela-planeta-partículas teste (representando o disco de detritos, sem considerar a auto-gravidade do disco nesta fase) para avaliar a estabilidade do disco ao longo da vida de Fomalhaut. Foram explorados seis cenários, combinando os planetas “Gap” e “Resonant” com duas configurações iniciais para o disco:

• Discos inicialmente circulares (e=0): Todas as partículas do disco começam em órbitas perfeitamente circulares.
• Discos inicialmente excêntricos (e ∝ a^-1): As partículas do disco começam com um perfil de excentricidade que diminui com a distância, consistente com as expectativas de modelagem.

As simulações foram executadas por 440 milhões de anos, a idade total de Fomalhaut (E. E. Mamajek 2012). Os resultados foram surpreendentes e extremamente reveladores.

Em todos os cenários onde os discos foram inicialmente circulares (C1, C2, C3), as simulações mostraram que esses discos não eram estáveis. As distribuições de partículas foram interrompidas, fragmentadas ou limpas pela interação com o planeta dentro de um período de tempo muito mais curto do que a idade de Fomalhaut (por exemplo, a simulação C1 foi interrompida em apenas 1 milhão de anos). Isso é inconsistente com as observações do disco de Fomalhaut, que claramente existe e é estável hoje.

Em contraste, os cenários onde os discos foram inicialmente excêntricos (E1, E2, E3) sobreviveram por todos os 440 milhões de anos da simulação. Eles resultaram em discos excêntricos que são consistentes com as propriedades observadas para Fomalhaut. Além disso, tanto o cenário do planeta “Resonant” quanto o do “Gap” esculpiram lacunas na região entre o cinturão principal e o intermediário, embora a lacuna fosse mais rasa para planetas de menor massa. Uma característica intrigante observada no cenário E1 (planeta ressonante maciço) foi a formação de uma onda de densidade espiral, que, embora ainda não observada em Fomalhaut, poderia ser detectada com observações de maior resolução no futuro.

6.1. O Legado do Disco Protoplanetário

As simulações N-corpos levam a duas conclusões de peso:

1. O disco de Fomalhaut pode ter se formado já excêntrico para sobreviver aos seus 440 milhões de anos de evolução. Isso implica que a excentricidade foi estabelecida durante a fase do disco protoplanetário da estrela, o estágio inicial de formação planetária.
2. Um único planeta pode ser responsável por esculpir as bordas do disco e as lacunas, mas pode não ser capaz de forçar sua própria excentricidade em um cinturão de planetesimais inicialmente circular para produzir um disco excêntrico com as propriedades de Fomalhaut. Ou seja, as interações planeta-disco teriam esculpido a morfologia do disco (suas bordas internas e lacunas), mas não teriam criado sua excentricidade.

Essa conclusão – de que discos excêntricos que sobrevivem até a sequência principal estelar podem ter sido produzidos durante a fase do disco protoplanetário – é consistente com trabalhos anteriores, como o de G. M. Kennedy (2020), que argumentou isso a partir da estreiteza aparente dos discos de detritos de Fomalhaut e HD 202628. De fato, já existem alguns discos protoplanetários excêntricos conhecidos, como MWC 758, HD 100546 e IRS 48.

Uma origem plausível para o disco excêntrico de Fomalhaut é que a excentricidade pode ter resultado da formação de um planeta (com propriedades consistentes com as da Tabela 2 do estudo) dentro do disco protoplanetário. Nesse cenário, as interações iniciais planeta-gás do disco teriam determinado o perfil de excentricidade do disco e a excentricidade do planeta. Um perfil de excentricidade que diminui com o raio é esperado nesse cenário, pois perfis planos ou crescentes com o raio tendem a sofrer precessão diferencial devido às forças de pressão do gás. Após a dissipação do gás do disco protoplanetário de Fomalhaut (e qualquer poeira primordial remanescente), as interações subsequentes planeta-disco com o cinturão de planetesimais excêntrico teriam plausivelmente esculpido as bordas internas e externas do disco, resultando na morfologia do cinturão ao longo de 440 milhões de anos, enquanto mantinham sua distribuição inicial de excentricidade (ou uma muito semelhante).

6.2. Física Adicional: O Papel da Auto-Gravidade do Disco

Embora as simulações N-corpos iniciais tenham assumido um disco de detritos sem massa, a realidade pode ser mais complexa. Efeitos físicos adicionais, como a influência de um disco de detritos massivo e auto-gravitante, podem afetar os resultados. Como mencionado anteriormente, um planeta dentro de um disco de detritos induz excentricidades planetesimais forçadas seculares, de modo que ef(a) ∝ a^-1 em um disco sem massa. No entanto, se o disco for massivo, sua auto-gravidade pode acentuar o perfil de excentricidade forçada, podendo chegar a ef(a) ∝ a^-4.5.

Isso ocorre quando as taxas de precessão apsidal (a mudança na orientação da órbita) induzidas pelo disco (ausentes em modelos de disco sem massa) dominam sobre a precessão induzida pelo planeta das órbitas dos planetesimais. Para o disco de Fomalhaut, as observações do ALMA implicam uma massa total do disco (incluindo os maiores planetesimais em colisão) que é consistente com a faixa inferida pela modelagem colisional (1.8–360 massas terrestres). Se isso for verdade, a gravidade do disco poderia potencialmente explicar o perfil íngreme de ef(a) (npow = -1.75 ± 0.16) indicado pela modelagem de Lovell et al., que é mais acentuado do que o ef(a) ∝ a^-1 esperado para um disco sem massa. Este é um campo fértil para futuras pesquisas, usando códigos seculares e N-corpos mais avançados que incorporem a auto-gravidade do disco.

Conclusão: Um Novo Olhar para o Passado e Futuro Cósmico de Fomalhaut

Chegamos ao fim de nossa jornada cósmica por Fomalhaut, e a vista é mais espetacular do que nunca! A equipe de Joshua B. Lovell e seus colaboradores nos presenteou com uma descoberta monumental: a primeira evidência inequívoca de um gradiente negativo de excentricidade no disco de detritos de Fomalhaut. Com um valor de npow = -1.75 ± 0.16, este gradiente não é apenas um detalhe técnico, mas a chave que destranca os mistérios das assimetrias observadas no disco, como seu brilho mais intenso no apocentro e sua largura maior no pericentro. Este fenômeno, carinhosamente apelidado de “Divergência de Velocidade Excêntrica” (EVD), é uma prova da elegância com que a física molda o universo.

Através de observações de alta resolução do ALMA e modelos paramétricos avançados, os pesquisadores demonstraram que a descrição do disco de Fomalhaut com este gradiente de excentricidade é estatisticamente superior a qualquer modelo que postule excentricidades constantes ou livres. Este não é apenas um avanço para Fomalhaut, mas um marco para a astronomia de discos de detritos como um todo, abrindo portas para uma nova era de compreensão de como esses cinturões cósmicos são formados e mantidos.

As implicações dessa descoberta se estendem à arquitetura planetária do sistema Fomalhaut. Embora nenhum planeta tenha sido detectado diretamente no momento, os modelos propostos pela equipe nos dão uma “impressão digital” dos planetas que poderiam estar atuando como arquitetos celestiais: seja um planeta “escultor de lacunas” a 109-115 au, ou um planeta “ressonante” a 70-75 au, ambos com massas e excentricidades que se encaixam nas observações e nas não-detecções atuais do JWST. A mera possibilidade de um planeta com características semelhantes ao controverso Fomalhaut b ser o responsável pela lacuna do disco é um lembrete fascinante de como a ciência avança.

Mas talvez a revelação mais profunda venha das simulações N-corpos. Elas nos contam uma história do passado de Fomalhaut: para que seu disco de detritos sobrevivesse por 440 milhões de anos, ele provavelmente nasceu já excêntrico. Isso significa que a semente da excentricidade foi plantada durante a fase do disco protoplanetário, com as interações planeta-disco agindo subsequentemente para esculpir a morfologia do disco, mas não para criar sua excentricidade fundamental. É uma visão poética da formação planetária, onde o destino de um disco pode ser traçado desde seus primeiros momentos.

Esta pesquisa não apenas aprofunda nossa compreensão de Fomalhaut, mas também nos lembra da beleza intrincada e da complexidade da formação de sistemas planetários. É um testemunho do poder da colaboração científica, da inovação tecnológica e da paixão incansável por desvendar os segredos do universo. O código usado para modelar este disco já está disponível publicamente, convidando outros cientistas a dar continuidade a essa linha de pesquisa.

O universo é um livro aberto, e cada nova descoberta é uma página virada que revela uma história ainda mais rica. A história de Fomalhaut e seu disco excêntrico é um convite para sonharmos, para questionarmos e para nos maravilharmarmos com a dança cósmica que acontece muito além da nossa pequena rocha azul. Compartilhe esta notícia com seus amigos, família e todos aqueles que amam o espaço. Vamos espalhar a fascinação pela astronomia e inspirar a próxima geração de cientistas e entusiastas a continuar desvendando os segredos do cosmos! O próximo capítulo desta saga estelar aguarda, e você faz parte dela!