
Um novo e abrangente estudo, publicado na revista Living Reviews in Relativity, destaca o papel revolucionário da relatividade numérica como uma ferramenta poderosa para desvendar os mistérios mais profundos da evolução do nosso universo. Intitulado “Cosmologia usando Relatividade Numérica“, este artigo de revisão oferece uma visão sem precedentes de como a simulação de ambientes de forte gravidade está transformando nossa compreensão da história cósmica, desde o Big Bang primordial até a distribuição de galáxias no universo tardio.
Por décadas, a cosmologia moderna tem se apoiado amplamente no Modelo de Friedmann-Lemaître-Robertson-Walker (FLRW), uma descrição que presume que o universo é perfeitamente homogêneo e isotrópico (uniforme em todas as direções e em todos os lugares) em grandes escalas. Embora este modelo tenha sido incrivelmente bem-sucedido e continue a ser a base para a cosmologia de precisão atual, ele tem suas limitações inerentes. O universo real, como observamos, não é perfeitamente liso; ele contém uma rica tapeçaria de estruturas – galáxias, aglomerados e vazios – que desafiam as premissas mais simples do modelo FLRW.
É precisamente aqui que a relatividade numérica (RN) entra em cena, atuando como um “microscópio cósmico” capaz de explorar as regiões do espaço-tempo onde a gravidade é tão intensa e as estruturas tão complexas que as aproximações tradicionais não são mais válidas. Esta ferramenta, já consagrada na astrofísica para simular eventos extremos como a fusão de buracos negros e estrelas de nêutrons, está agora sendo aplicada para resolver algumas das questões mais desafiadoras da cosmologia.
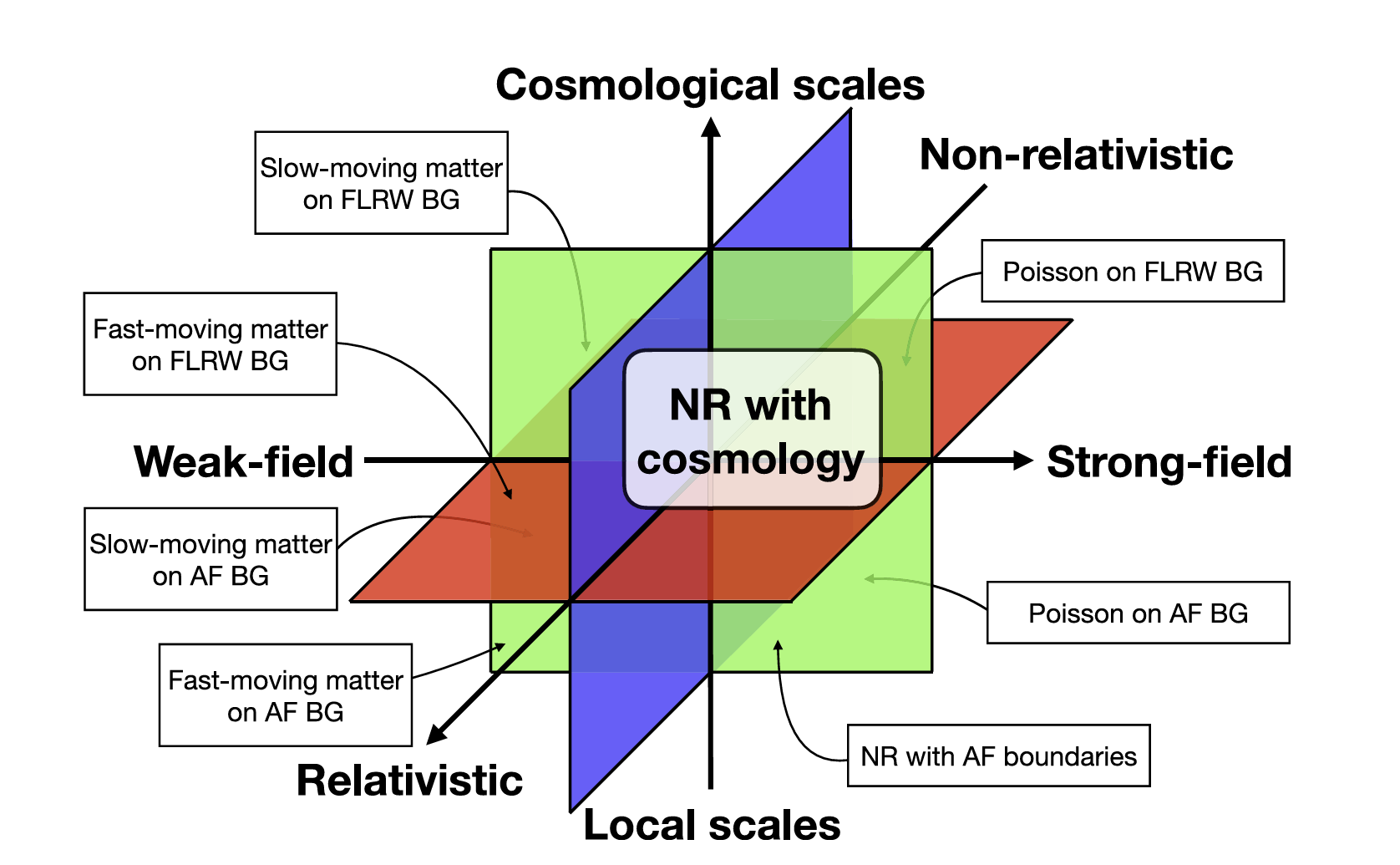
Por Que Precisamos da Relatividade Numérica na Cosmologia?
A necessidade de ir além das descrições simplificadas do universo surge quando certas condições são atendidas:
- Reação Local Significativa: Quando as inhomogeneidades na densidade da matéria são grandes, ou seja, onde a variação de densidade é comparável à densidade média. Nestes casos, a gravidade local se torna extremamente relevante, influenciando diretamente a dinâmica do espaço-tempo.
- Inomogeneidades Coerentes em Escalas de Hubble: Se estas inhomogeneidades se estendem por distâncias equivalentes à escala de Hubble (a distância onde a velocidade de recessão de uma galáxia excede a velocidade da luz devido à expansão do universo), ou persistem por um tempo de Hubble (o inverso da taxa de expansão), as aproximações lineares falham.
- Ausência de Simetrias: Em situações onde o espaço-tempo é dinâmico e não possui as simetrias simples que permitiriam simplificações no cálculo, a RN se torna indispensável. Por exemplo, a formação de buracos negros primordiais ou a colisão de bolhas inflacionárias são eventos que carecem de tais simetrias.
A RN permite simular a evolução completa da relatividade geral, sem as simplificações de fundo, conformidade plana ou abordagens perturbativas. Isso é crucial para investigar fenômenos onde os efeitos não-lineares da gravidade são dominantes, como a formação de singularidades cosmológicas, os mecanismos da inflação e da contração lenta que visam suavizar os espaços-tempos inicialmente desiguais, e a dinâmica não-perturbativa no reaquecimento ou na formação de buracos negros primordiais (PBHs).
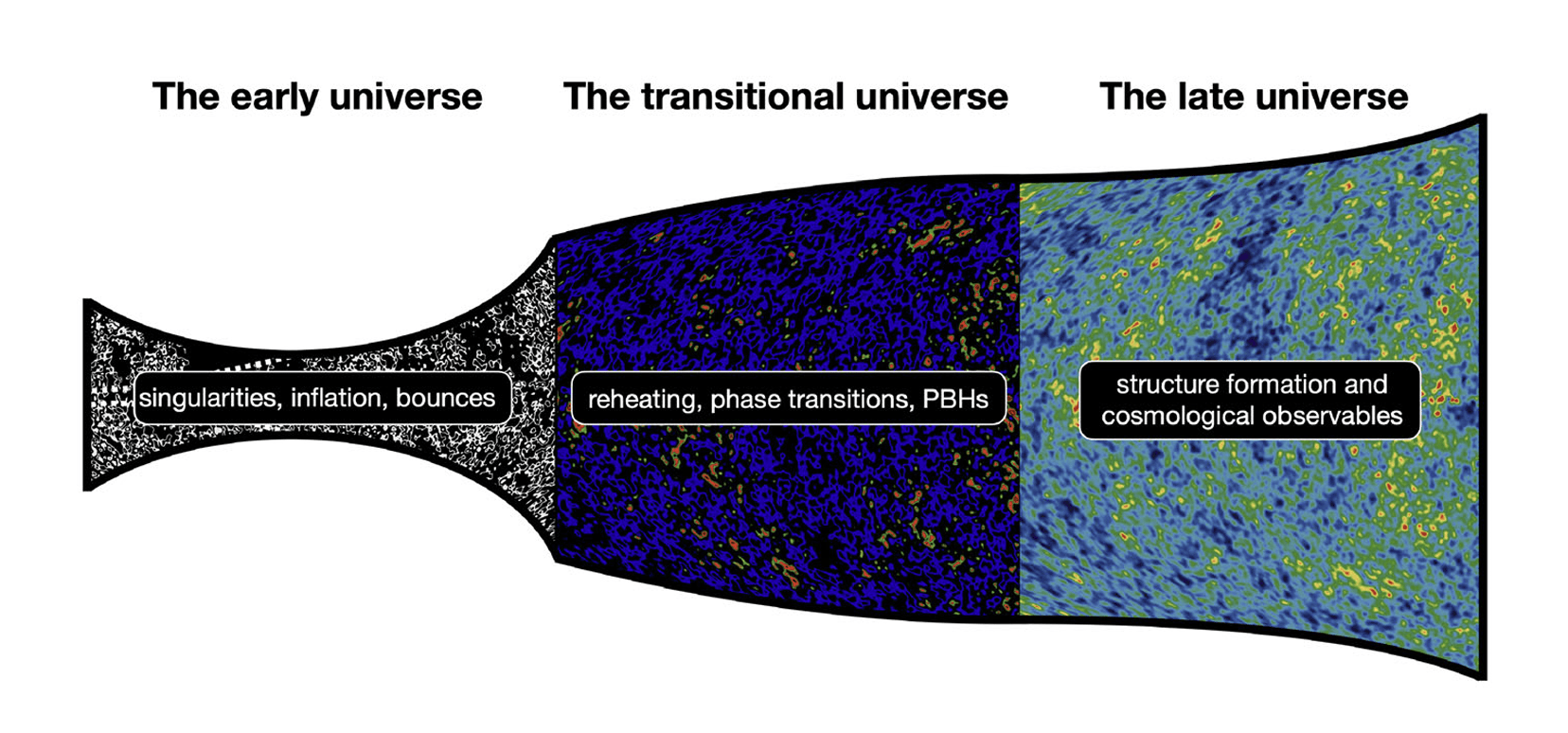
Viagem Através da História Cósmica com a Relatividade Numérica
O estudo divide as aplicações da relatividade numérica na cosmologia em três grandes eras, seguindo a linha do tempo do universo:
1. O Universo Primordial: Desvendando o Início do Tempo
Esta seção aborda as questões mais distantes no passado do universo, explorando como ele pode ter começado e como um universo inicialmente não-homogêneo pode ter evoluído para a uniformidade que observamos hoje.
- Singularidades Cosmológicas e Universos Mixmaster: A teoria da relatividade geral de Einstein prevê que, ao rebobinar o tempo do nosso universo, inevitavelmente chegaremos a uma singularidade – um ponto onde as leis da física como as conhecemos se quebram. No entanto, a natureza exata dessa singularidade não é especificada pelos teoremas de singularidade de Penrose. A Conjectura BKL (Belinskii, Khalatnikov, Lifshitz) sugere que a singularidade em colapsos gravitacionais genéricos é espacial, local e oscilatória, semelhante aos universos Mixmaster (Bianchi tipo IX). Nesses cenários, o espaço-tempo passa por uma série de transformações caóticas e discretas entre diferentes “épocas de Kasner”, onde uma direção se expande enquanto outras duas se contraem. As simulações de RN têm fornecido evidências numéricas consistentes com a conjectura BKL, mostrando que, para a maioria das configurações iniciais genéricas, a dinâmica de Mixmaster é o resultado mais comum, a menos que a matéria, como um campo escalar, possa dominar e suprimir esse comportamento caótico. Esses estudos também revelaram a existência de “espigões” — superfícies bidimensionais onde os gradientes crescem arbitrariamente, mas cujo impacto geral diminui à medida que a singularidade é abordada, mantendo a validade do cenário BKL. A aplicação da RN para investigar essas singularidades inspirou novas técnicas numéricas, como a formulação de tétrade, que se provou útil em outras áreas da RN, como as simulações de buracos negros binários.
- Inflação e o Problema das Condições Iniciais: A inflação cósmica é uma teoria proeminente que postula um período de expansão quase exponencial no início do universo. Esta fase é proposta para explicar por que o universo é tão plano, homogêneo e isotrópico em grandes escalas, apesar de uma singularidade inicial que poderia ser caótica e descorrelacionada. A inflação também oferece um mecanismo para gerar as perturbações primordiais que semearam a formação de estruturas. Uma questão crucial é se a inflação é “robusta” – ou seja, se ela pode ocorrer a partir de condições iniciais suficientemente genéricas e desiguais. Simulações de RN têm abordado esta questão, mostrando que, para a inflação de alta escala (onde a energia da inflação é muito alta), o processo pode ocorrer mesmo na presença de grandes inhomogeneidades e formação de buracos negros. No entanto, modelos de inflação de baixa escala (com menor energia) parecem ser menos robustos a tais perturbações. A pesquisa também investigou o impacto da velocidade inicial do inflaton (o campo escalar que impulsiona a inflação) e de múltiplos campos escalares, geralmente concluindo que a inflação permanece robusta, embora a distribuição de e-folds (o número de dobramentos do tamanho do universo) possa variar. A RN também está começando a ser usada para explorar como modificações de alta energia à relatividade geral afetam a inflação.
- Cenários Ekpiróticos e de Salto (Bounce): Uma alternativa à inflação para explicar a homogeneidade do universo é o modelo ekpirótico e seus cenários de salto. Nestes modelos, o universo passa por uma fase de contração lenta que suaviza as inhomogeneidades, antes de sofrer um “salto” não-singular para uma fase de expansão, que se torna o Big Bang quente. Para que um salto ocorra, é necessário violar a condição de energia nula (CEN), o que geralmente requer física nova ou matéria exótica, como um campo escalar fantasma. As simulações de RN mostraram que a fase de contração lenta pode, de fato, suavizar eficientemente o universo, transformando regiões inicialmente desiguais em homogêneas e isotrópicas. No entanto, a introdução de campos adicionais para gerar as perturbações de escala invariante (necessárias para a formação de estruturas) pode introduzir instabilidades. A RN também investigou o comportamento de buracos negros durante esses saltos, descobrindo que eles podem temporariamente fundir e desaparecer durante a fase de contração, apenas para ressurgir na fase de expansão.
- Assinaturas de Colisões de Bolhas Inflacionárias: Alguns modelos de inflação predizem a existência de um multiverso, onde o nosso universo é apenas uma de muitas “bolhas” em um espaço inflacionário maior. Colisões entre essas bolhas poderiam deixar assinaturas observacionais distintas na Radiação Cósmica de Fundo (CMB), como anisotropias de temperatura. As simulações de RN foram cruciais para modelar essas colisões, que são intrinsecamente não-lineares e dinâmicas. Estudos em 1+1 dimensões com simetria SO(2,1) revelaram que a estrutura do potencial escalar é mais importante do que a cinemática da colisão para determinar o resultado. Eles mostraram que colisões podem formar “oscilões” (configurações localizadas de campo escalar) e bolsões de falso vácuo, e que poderiam perturbar a inflação em modelos de campo pequeno, mas não em modelos de campo grande. Pesquisas mais recentes estabeleceram conexões quantitativas entre os modelos inflacionários e as assinaturas da CMB, como a aniso-tropia de temperatura azimutalmente simétrica. O sinal resultante (uma mancha quente ou fria na CMB) depende de se as bolhas são idênticas ou não e de como o campo escalar reage à colisão.
2. O Universo de Transição: Reaquecimento, Defeitos e Buracos Negros Primordiais
Esta era cobre fenômenos de forte gravidade que podem ter ocorrido quando o universo já era aproximadamente homogêneo e isotrópico em grandes escalas, mas antes que as estruturas de grande escala começassem a dominar.
- Reaquecimento e Formação de Oscilões: Após a inflação, o universo precisa transitar para uma era dominada por radiação – o reativação (reheating). Este processo, especialmente o pré-reaquecimento (preheating), envolve dinâmicas não-perturbativas, onde a energia do inflaton (o campo que impulsionou a inflação) é convertida em outras partículas leves. O pré-reaquecimento é inerentemente não-linear e está longe do equilíbrio térmico. As simulações de RN comparam os resultados de modelos simplificados (teoria de perturbação linear, teoria de campo em rede em um fundo FLRW rígido) com as dinâmicas completas campo-espaço-tempo da RN. Estudos iniciais em 1+1 dimensões mostraram que efeitos gravitacionais não-lineares podem transferir energia entre modos ressonantes e não-ressonantes e até mesmo levar ao colapso gravitacional em regiões superdensas. As simulações 3+1D confirmaram que a amplificação de modos em super-horizonte persiste e que a produção de ondas gravitacionais pode ser significativamente maior quando a relatividade geral completa é incluída. Um resultado notável do pré-reaquecimento é a formação de oscilões: configurações localizadas, massivas e metaestáveis de campo escalar. A RN tem sido usada para entender se os resultados de simulações mais simples ainda se aplicam, qual é o espectro de ondas gravitacionais (OGs) emitidas por esses objetos e se eles podem colapsar em buracos negros. Simulações recentes com RN mostraram que as correções da relatividade geral levam à formação de oscilões mais numerosos e densos. No entanto, apesar de altas densidades, a compactação máxima dos oscilões geralmente não é suficiente para que eles colapsem em buracos negros, indicando que a pressão interna dos campos desempenha um papel importante. A extração de OGs do pré-reaquecimento também é um desafio, com as simulações mostrando que os resultados são altamente sensíveis à escolha da “calibragem” (gauge) numérica, enfatizando a necessidade de abordagens cuidadosas para obter previsões observacionais precisas.
- Transições de Fase e Defeitos Topológicos: À medida que o universo esfriou, ele provavelmente passou por transições de fase que deram origem às forças fundamentais que conhecemos hoje. Durante essas transições, podem ter surgido defeitos topológicos, como paredes de domínio, cordas cósmicas e monopólos, dependendo da simetria do vácuo. A RN tem sido utilizada para estudar a evolução de bolhas de vácuo e como as inhomogeneidades podem preencher o “landscape” de múltiplos vácuos. A dinâmica dessas bolhas pode atuar como sementes para buracos negros supermassivos e aumentar a formação de buracos negros binários. Embora as cordas cósmicas sejam fenômenos importantes que também geram OGs, a enorme separação de escalas envolvidas torna sua simulação em RN um desafio contínuo, muitas vezes exigindo aproximações simplificadas. A pesquisa está em andamento para desenvolver técnicas mais sofisticadas para modelar esses objetos.
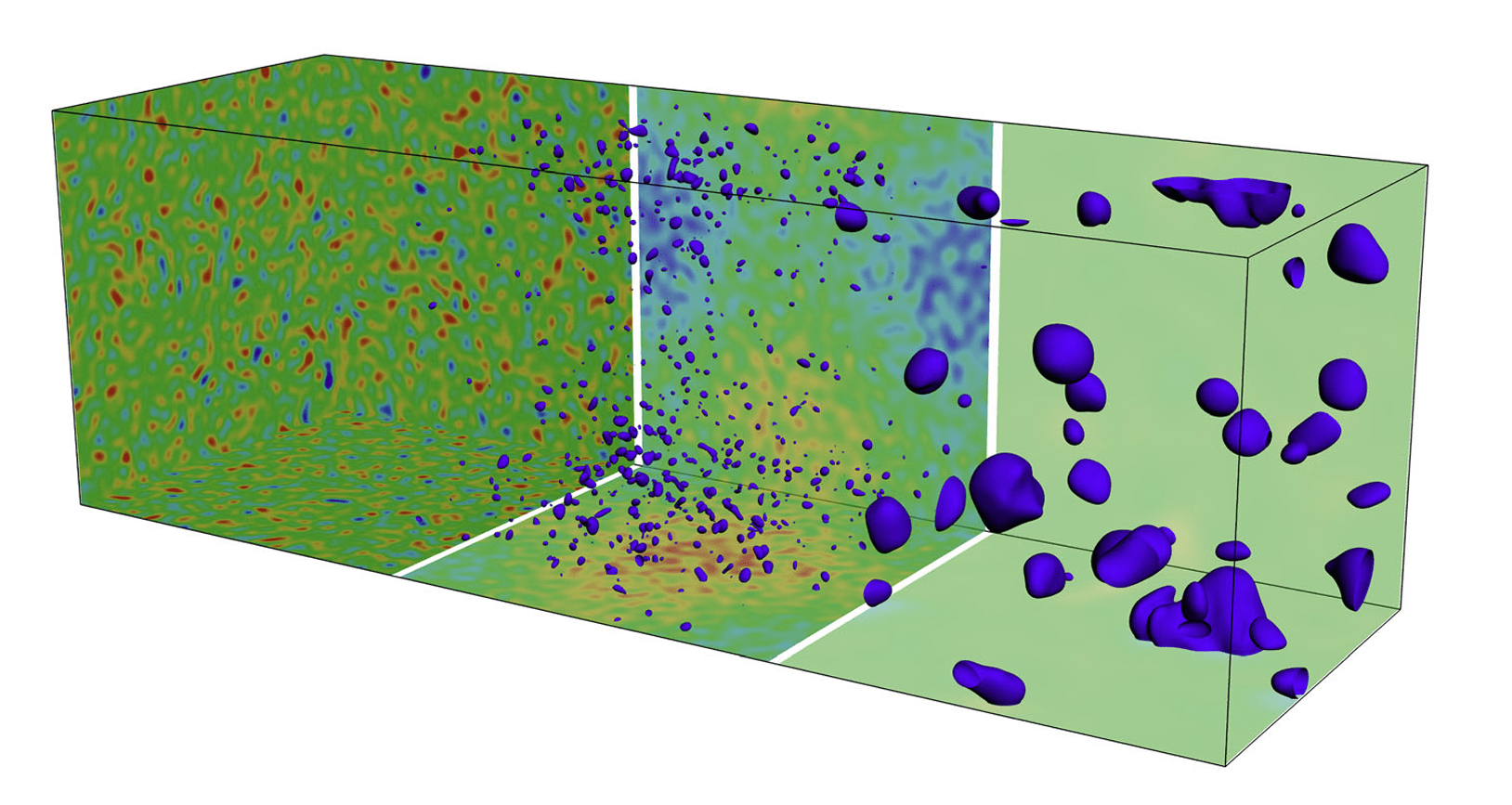
- Buracos Negros Primordiais (PBHs): Os PBHs são uma classe fascinante de buracos negros que poderiam ter se formado nos primeiros momentos do universo a partir do colapso de flutuações de densidade extremamente grandes, geradas durante ou logo após a inflação. Eles são candidatos para a matéria escura ou sementes para buracos negros supermassivos. A determinação precisa do limiar crítico de densidade para a formação de PBHs é vital, pois pequenos erros podem levar a grandes variações no número previsto de PBHs. Simulações de RN têm refinado as estimativas analíticas iniciais (como o limiar de ~1/3 proposto por Carr e Hawking), mostrando que o limiar efetivo para a formação de PBHs em um universo dominado por radiação está na faixa de 0,3 a 0,5. Os estudos iniciais sobre a formação de PBHs usavam modelos simplificados de simetria esférica. A RN permitiu investigar a formação de PBHs em contextos mais complexos, incluindo a aplicação de comportamento crítico de escala, semelhante ao descoberto por Choptuik para o colapso gravitacional, onde a massa do buraco negro formado segue uma lei de potência perto do limiar de colapso. Estudos recentes em 3+1 dimensões (mais realistas, sem a restrição de simetria esférica) com RN estão explorando o efeito de perturbações não-esféricas na formação de PBHs, bem como a rotação resultante. Embora as perturbações elípticas pareçam ter um impacto desprezível no limiar em situações padrão, e o spin final dos PBHs formados na era dominada por matéria seja geralmente insignificante devido à acreção do ambiente circundante, a RN continua a ser uma ferramenta essencial para aprimorar as previsões sobre a formação e as propriedades dos PBHs.
3. O Universo Tardo: Efeitos Relativísticos na Estrutura de Grande Escala
Esta última fase explora a evolução cosmológica após a era de igualdade matéria-radiação, onde as observações de estrutura de grande escala nos ajudam a sondar os parâmetros cosmológicos e a física fundamental.
- Reação e Média em Espaços-Tempos Não-FLRW: A maioria dos estudos da estrutura de grande escala utiliza simulações que assumem gravidade newtoniana em um fundo FLRW em expansão. No entanto, há um interesse crescente em quantificar os efeitos da “reação” (backreaction) – como as inhomogeneidades em pequena escala podem influenciar a evolução em grande escala do universo. A RN permite abordar diretamente esta questão. Trabalhos iniciais sistemáticos usando códigos de RN como CosmoGRaPH e Einstein Toolkit, modelando a matéria como um fluido sem pressão, mostraram que, embora as inhomogeneidades possam ser grandes, o desvio do modelo FLRW é surprisingly pequeno – da ordem de 0,3% para o parâmetro de expansão local, mesmo com perturbações iniciais significativas. No entanto, em escalas menores, como as de levantamentos de galáxias locais, desvios de até 6% da homogeneidade podem ocorrer. Uma das descobertas mais importantes é que a separação de escalas é robusta na evolução cosmológica: a não-linearidade da relatividade geral não induz acoplamentos onde modos de pequena escala afetam significativamente a evolução cosmológica em grande escala. Isso implica que a relatividade geral completa não é, por si só, suficiente para explicar a aceleração observada da expansão do universo através de efeitos de reação. No entanto, a RN ainda é crucial para entender sistemáticas e efeitos percentuais que podem ser relevantes para as futuras observações cosmológicas de precisão.
- Observáveis Cosmológicos no Regime Não-Linear: Embora as simulações de N-corpos baseadas na gravidade newtoniana sejam surpreendentemente precisas para a maior parte da evolução cosmológica tardia, a RN desempenha um papel vital como ferramenta de validação e para investigar efeitos sutis de relatividade geral que poderiam ter implicações observacionais.
- Lentes Gravitacionais Fracas: A RN tem sido usada para calcular o espectro de potência de lentes gravitacionais fracas, que muitas vezes dependem de aproximações. Estudos de RN indicaram que a “aproximação de Born” (onde os raios de luz são assumidos como não perturbados por efeitos gravitacionais de ordem superior) pode levar a erros de nível percentual em certas escalas angulares, destacando possíveis sistemáticas não capturadas por teorias de perturbação de ordem superior.
- Variação Cósmica e Medidas Locais: Simulações de RN têm investigado o impacto de amostras de céu anisotrópicas na medição do parâmetro de Hubble e seus momentos superiores. Elas revelaram que a variação cósmica – as diferenças nas medições devido à localização específica de um observador em um universo heterogêneo – pode levar a diferenças percentuais nas medições do parâmetro de Hubble. Por exemplo, um observador pode ter 7% de probabilidade de medir uma diferença de até 3% no parâmetro de Hubble de um universo típico de Einstein-de Sitter.
- Vazios e Curvatura Espacial: A RN também tem explorado o impacto de vazios (regiões de baixa densidade) e outras inhomogeneidades próximas nas inferências dos observadores sobre a constante de Hubble. Os vazios são geralmente negativamente curvados, e suas estatísticas de tamanho seguem aproximadamente as de simulações de N-corpos.
- Desvio para o Vermelho (Redshift Drift): Um observável de interesse é o desvio para o vermelho, onde o desvio para o vermelho de um objeto evolui com o tempo devido à expansão cósmica. A RN prevê que as flutuações no desvio para o vermelho devido a inhomogeneidades podem estar no nível de 10% em baixos desvios para o vermelho (z=0.1), potencialmente observáveis em levantamentos espectroscópicos de próxima geração.
- Arrasto de Quadro (Frame Dragging): A RN está sendo usada para investigar o arrasto de quadro, um efeito relativístico que causa a rotação de sistemas de coordenadas locais devido à distribuição de massa e momentum.
- Curvatura Espacial: A RN está ajudando a sonda a questão da curvatura espacial em um universo heterogêneo. Simulações mostraram que as inhomogeneidades introduzem uma curvatura espacial efetiva da ordem das perturbações, que pode ser de até 10%.
Desafios Atuais e Direções Futuras
A relatividade numérica é uma ferramenta em constante evolução, e a sua aplicação na cosmologia apresenta desafios únicos:
- Condições de Contorno e de Calibragem (Gauge) Otimizadas: A escolha de como definir as bordas de uma simulação (condições de contorno) e como rastrear o tempo e o espaço (escolha de calibragem ou gauge) pode impactar significativamente os resultados. Desenvolver condições de calibragem mais bem adaptadas a espaços-tempos cosmológicos distantes do modelo FLRW é uma área ativa de pesquisa.
- Acesso a uma Gama Mais Ampla de Escalas Físicas: Simular a evolução de objetos com escalas muito diferentes (como uma corda cósmica extremamente fina em um universo vasto) é um desafio computacional.
- Diagnósticos para Espaços-Tempos Inomogêneos: A interpretação de quantidades em um universo não-uniforme é complexa. O que é uma “média” em um universo em evolução? A RN está desenvolvendo ferramentas para rastrear observadores geodésicos (que se movem livremente sob a gravidade) para obter medidas mais fisicamente significativas.
- Quantificação Precisa de Ondas Gravitacionais: A extração de sinais de ondas gravitacionais de simulações cosmológicas é sensível às escolhas de calibragem e requer metodologias robustas para garantir a precisão.
- Condições Iniciais Físicamente Corretas: Garantir que os dados iniciais das simulações não apenas satisfaçam as equações de Einstein, mas também representem cenários astrofísicos ou cosmológicos realistas, é um problema complexo. A limitação de assumir um espaço “conformemente plano” (com uma forma geométrica simples) ainda é uma área a ser superada.
- Ferramentas de Código Aberto: A disponibilização de ferramentas de código aberto e de propósito geral para a comunidade científica reduziria a barreira para novos pesquisadores e aceleraria o progresso na área.
Conclusão
A relatividade numérica está se estabelecendo como um pilar essencial na pesquisa cosmológica, abrindo caminhos para explorar épocas e fenômenos do universo que são inacessíveis a outras metodologias. Desde a natureza caótica das singularidades do Big Bang e a robustez da inflação diante de condições iniciais extremas, passando pelas complexas dinâmicas de reaquecimento e a formação de buracos negros primordiais, até os efeitos sutis da gravidade em larga escala na observação do universo tardio, a RN está nos fornecendo uma imagem mais completa e precisa da nossa realidade cósmica.
Embora ainda existam muitos desafios técnicos e conceituais a serem superados, o campo está em rápido crescimento, prometendo descobertas futuras que continuarão a moldar nossa compreensão do cosmos. A colaboração entre cosmologistas e especialistas em relatividade numérica será fundamental para desvendar os próximos capítulos da história do universo, incluindo a exploração da cosmologia com gravidade modificada, o entendimento da cosmologia de cordas e a simulação de redes de cordas cósmicas gravitantes.
Este é apenas o começo de uma jornada emocionante na qual a cosmologia numérica nos levará a fronteiras ainda mais distantes do conhecimento cósmico.






Comente!